
1. Taguchi Genichi
4번째 포스팅은 다구찌(Taguchi) 의 품질공학에 대한 얘기입니다. TMI로는 제가 좋아하는 교수님께서 다구찌 방법을 좋아하셨습니다. 그래서 저의 품질철학에도 영향을 많이 받았습니다. 다구찌의 품질공학 은 설계 방법론이자, 개선 방법론입니다.
먼저 가볍게 이야기하면, 대부분의 사람들은 품질에 대해 두 가지를 생각합니다. 첫 번째는 불합리한, 불필요한, 비효율적인 요소를 줄이면 좋은 제품이 만들어 진다. 두 번째는 기존 성능을 최대화시키자, 성능을 더 상향시키면 좋은 제품이 나온다.
1.1. Case study : SONY
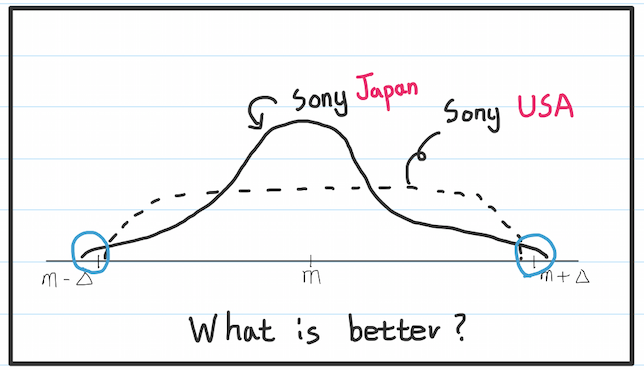
Spec-In 이면 다 정상제품이냐!
어떻게 생각하세요? 제품을 만들 때는 늘 허용오차(Tolerance)가 존재합니다. 30cm 자를 만드는데, 30cm자의 길이를 재보니까 30.001cm 에서 29.999cm까지의 범위에 들어온다면, 제품으로 팔겠다고 얘기합니다. 당연히 정밀도를 올리면 제품 생산 비용이 올라가다보니 적정선에서 타협을 해야됩니다. 그러나 다꾸찌는 이런 생각은 잘못됐다고 얘기합니다. 위 사진처럼 범위 안에 들어오더라도, 평균에 집중되도록 제품을 만들어야 된다고합니다. 즉, 30cm 자를 만들 때에는 정확한 30cm를 목표치로 봐야합니다. 평균치, 공칭치, 대표치가 아니라는 얘기죠. 왜냐하면 허용오차라는게 생산자가 만들어낸 타협점이지 고객은 제품에 대한 허용오차를 정의한 적도 없거니와 이해하지 않습니다.

저의 일화로 얘기하자면 제트플립 톰브라운을 사용했었습니다. 그냥 제트플립을 쓰는 친구와 비교해보니까, 접었다 펼 때 느낌이 제법 다르더라구요. 제가 좀 더 부드럽다고 생각했습니다. 그런데 다른 사람은 헐렁거린다고 얘기하더라구요. 전 이 비교를 하기 전까지는 생활에 큰 불편을 느낀 적이 없었습니다만, 그 뒤부터는 불량인가? 고민을 하곤 했습니다. 허용오차의 영역이지만 쓰는 소비자입장에서 기분 나쁘면 마음을 돌아서게 됩니다. 심하면 브랜드 밸류에도 영향을 주죠. 다른 이유가 큽니다만 저는 지금 아이폰12를 쓰고 있습니다. 제 경우만 봐도 생산자 입장에선 많이 억울하고 괴로울 겁니다.
1.2. Loss function

그래서 다꾸찌는 손실함수(Loss function) 에 대해서 다시 정의합니다. 이때까지는 대부분 사람들이 Spec-In 이면 손실없다고 생각을 했는데, 이는 잘못됐으며 목표치와 멀어질수록 2차 함수의 형태로 손실비용이 증가한다고 얘기합니다.
1.3. Minimize sigma, Maximize target

설계변수와 성능특성간의 관계를 나타낸 반응곡선입니다. x 축의 설계변수를 잘 따라가다보면 y 축의 산포가 좁은 구간이 나옵니다. 다시 30cm 자를 비교해보면, 30cm를 잘라보니 0.001의 정밀도가 나옵니다. 15cm로 잘랐을 때는 동일 비용에 0.0001의 정밀도가 나온다고 친다면, 이유가 있겠죠. 그러면 설계팀에서 고민을 합니다. 15cm 자를 만들어서 팔면 되겠다 는 농담이고 15cm에서 나오는 반응을 30cm에서도 나오게 끌어오자 즉, 산포를 줄이고 평균을 올려서 품질을 올릴 수 있다는 것이 다꾸찌 품질공학의 철학입니다.
1.4. Robust design

지금은 사실 이해하기 힘들지만, 예전에는 설계 단계에서 세워지는 이론들과 가정이 현실과 어울리지 않았습니다. 별 다른 환경변수가 고려되지 않아서 그랬고 이를 처음으로 생각한 것이 다꾸찌의 강건설계 입니다.

유리를 예로 들겠습니다. 유리를 가열한 다음 굳히면서 모양을 잡습니다. 그러다보니 이러한 성형과정에서는 가능한 빨리 녹이는게 관건입니다. 위 이미지를 보면 온도의 변화에 빨리 반응하는 자재를 쓰는 것이 앞으로 만들어질 목표치에 집중할 수 있겠죠. 추가적으로 얘기하는 강건설계(Robust design) 은 항상 많은 비용을 필요로 하는 것이 아닙니다. 당연히 엄청난 비용을 쏟으면 높은 정밀도로 좋은 제품이 나오겠죠. 강건설계 의 핵심은 원인을 항상 제거할 필요없이 상호작용을 최소화할 수 있음에 대한 가능성을 보여준다는 것입니다.
1.4.1. Robustness
강건성(Robustness) 은 제품 성능이 여러 변수에 영향을 덜 받는 수치입니다. 최소 단위의 제조 비용을 신경써야하고 노이즈에 대해서도 잘 파악해야 합니다. 강건설계 (Robust design) 는 위에 얘기했던 것처럼 원인을 항상 제거할 필요는 없고, 상호작용을 최소화할 수 있으며 위의 Loss function 에서 얘기한 것처럼 목표치에 벗어나는 그 순간부터 손실이 발생한다고 얘기합니다.
1.5. Quality Characteristic Value

다꾸찌는 품질특성치(Quality Characteristic Value) 를 동특성(Dynamic characteristic)과 정특성(Static characteristic) 으로 나눴습니다. 동특성 은 제품 군 전체에 대한 범용적인 특성을 얘기하고 이를 기술 개발시 중요한 원류품질 특징이라 합니다. 정특성 은 특정한 제품에 보여지는 특성을 얘기하고 이를 설계시 중요한 상류품질 이라고 얘기합니다. 특히 이중에서 정특성 은 특정 제품에 국한되는 특성이다 보니, 망목특성, 망소특성, 망대특성 으로 구분됩니다.
| 이름 | 내용 | 비고 |
|---|---|---|
| 망목특성(Target the better) | 특성치가 목표치에 일치할수록 좋은 경우 | X bar - R 관리도의 목적 |
| 망소특성(Smaller the better) | 특성치가 작을 수록 좋은 경우 | 특성치는 음수가 없어, 0에 가까워야 함 |
| 망대특성(Larger the better) | 특성치가 클 수록 좋은 경우 | B10 수명을 통한 관리 |
마지막으로 Dynamic, Static 을 구분하다보니, 동특성은 입력신호에 따라 출력이 조절할 수 있는 특성이 이고 정특성은 위 표처럼 일정한 목표값을 내는 것으로 봅니다.
1.6. Loss function about static characteristic

이 수식에서 k는 큰 의미를 가지지는 않습니다만, 학습을 위해 설명하자면 평균m을 기준으로 양측 델타 에 들어가는 손실비용 W 를 얘기합니다. 여기서 k 는 손실비용 W 를 델타 제곱으로 나눈 값을 의미합니다. 델타 범위 모여있는 손실비용의 단위개념이죠.
2. Quality Engineering

우리는 일상에서 많은 제품을 쓰고 있습니다. 침대에 일어나서, 씻고 연락하고 밥을 먹고 이동하고 다시 집에 들어와 옷을 걸어놓는 것까지, 하루에 사용하는 제품들 중에서 불편한 것도 있고 맘에 드는 것도 있습니다. 그리고 우습게도 당연히 잘 쓰다보니 이게 좋은 제품이었구나 깨닫기 힘든 것도 있습니다. 참고로 중국출장가서 쓰던 임시 핸드폰은 전화가 길어지면 발열이 심해져 전화가 강제로 끊어졌습니다.
사용자 입장에선 많이 생산하는 것은 관심도 없고 기업 이미지와도 상관없습니다. 품질은 얘기가 다릅니다. 프리미엄 브랜드가 늘 대규모로 오래 살아남는 이유기도 하죠. 품질공학(Quality Engineering) 은 사용자의 환경에 상관없이 기능이 안정되도록, 그리고 가장 경제적이도록 설계 조건을 최적화 하는 학문입니다.
2.1. Purpose
품질공학의 목적은 아래와 같이 정의합니다.
- 개발기간의 단축
- 제품, 공정설계의 최적화
- 사용자 환경에서의 기능 안정화
- 기술개발의 선행성, 범용성, 재현성 확보
- 저비용, 고품질, 빠른 납기 보증
품질공학 은 생산라인 을 기준으로 라인 외 품질관리(Off-Line QC) , 라인 내 품질관리(On-Line QC) 로 나뉩니다. 이 둘을 나누는 기준은 설계영역 이냐, 관리영역 이냐로 구분하기 위해서 입니다. 라인 외 는 설계영역 라인 내 는 관리영역 입니다.
2.2. Taguchi designed experiment
다구찌의 실험에는 세 단계가 있습니다.
| 단계 | 명칭 | 내용 |
|---|---|---|
| 제 1단계 | 시스템 설계(System Design) | 고유기술, 전문지식, 경험 등을 바탕으로 제품 기획에서 넘어온 Proto type을 개발 |
| 제 2단계 | 파라미터 설계(Parameter Design) | 노이즈의 영향 속에서 성능 특성치의 분산을 적게, 평균은 높게 설계변수 조건 설정 |
| 제 3단계 | 허용차 설계(Tolerance Design) | 파라미터 설계에 의해 정해진 조건에서도 산포가 만족할만한 상태가 아닌 경우 공정변수 혹은 부품을 선택하여 허용차를 줄여주는 것 |
다구찌는 품질관리 활동 은 주로 제품설계에서 이뤄지고 늦어도 공정설계에서 이뤄져야한다고 합니다. 즉 라인 외 품질관리 에서 해야지 진정으로 품질을 올릴 수 있다는 것이죠. 라인 내 품질관리 에서 본다면, 검사와 공정관리를 통해서 변경 못하는, 고질적인, 고유 특성들은 건드릴 수 없다는 내용을 담고 있습니다. 손실 함수 와 강건 설계 를 얘기해보면, 결국 높은 품질의 제품이 손실이 적기에, 목표치에서 변동이 적도록 강건하게 설계해야 합니다.
그래서 다구찌의 실험방법 에는 직교표(orthogonal table) 을 이용한 실험과 SNR(Signal-to-Noise Ratio) 의 분석이 있습니다.
3.1. Orthogonal Arrays

딱 필요한 만큼만 실험을 할 수 있게 알려주는 직교배열법입니다. 이 표를 통해서 실험을 계획하고 관리하기가 쉽습니다. 이 직교배열표 는 정해진 메커니즘에 의해서 일부 실시법, 분할법, 교략법 등의 배치를 쉽게 할 수 있습니다. 또한 실험의 크기를 키우지 않고도 실험에 많은 인자를 투입할 수 있어 효율적입니다. 만들어진 직교배열표를 이용하여 실험을 하면 결과의 재현성이 높습니다. 많은 인자를 동시에 조합하여 취급하기 때문이죠. 같은 이유로 바람직한 최적조건이 결정됩니다. 그러나 이런 조합을 통해 오차가 클 수가 있는데요. 이 오차를 커버할 수 있는 통계적 해석이 들어가기에 일반적으로 큰 오차에도 실험 결론에 영향이 없습니다.
표준 직교배열표 : 한 수준 인자의 표준 직교 배열
확대 직교배열표 : 교호작용을 무시하고 많은 인자들만을 배치하여 실험할 수 있도록 만든 직교배열표
혼합 직교배열표 : 다른 수준의 열이 혼합된 직교배열표, 주효과만을 취득하고 싶을 때 사용(여러 종류의 수준 인자 혼합)
응용 직교배열표 : 표준 직교배열표에서 다수준 작성법에 수준을 바꿔 열을 갖추는 직교배열법
| 수준 | 경우의 수를 설명, 2수준계 인자 - 1, 2 3수준계 인자 - 1, 2, 3 4수준계 인자 - 1, 2, 3, 4 |
| 교호작용 | 열과 열의 조합 a, b, c의 경우 교호작용 ab, ac, bc, abc |
| 자유도 | 교호작용을 나타낼 수 있는 수 |
통계학에서 말하는 자유도는 주로 주어진 조건에서 자유롭게 변화할 수 있는 수에 해당된다. 주로 분산을 구할 때 n-1을 쓰는 이유도 n 개의 데이터를 가진 벡터들은 각 차원들이라 차원들간의 쌍을 붙여본다면 n-1이 나오기에 큰 맥락으로 봐서는 위의 자유도와 같습니다.
3.2. Expression

수준, 수준계 :

주효과는 점, 교호작용은 선
3.2.1. 표준 직교배열표

3.2.2. 확대 직교배열표

3.2.3. 혼합 직교배열표

3.3. Placement
직교배열표를 쓴다는 것 자체가 적은 실험횟수로 특성치에 영향을 주는 주요인자들을 걸러내는 작업이 목적입니다. 그러다보니 수준의 수는 대부분 2, 3수준계에서 머무르죠. 그러다보니 인자의 수준 선택은 확실한 방향으로 1수준, 현 공정조건을 넣어 2수준, 여기서 불안하다면 양방향에서 1수준씩 채택하여 3수준을 선택할 수 있습니다. 어쨌든 한번 배치해볼까요
3.3.1. 교호작용이 없는 경우

교호작용이 없으면 주효과만을 구하는 경우이기에 단순하게 배치할 수 있습니다. 먼저 자유도를 구한 다음, 그 자유도에 해당하는 표를 찾아 순서대로 대입합니다. 그리고 남은 배치에는 에러항으로 구분합니다.
3.3.2. 교호작용이 있는 경우

교호작용이 있으면 매핑 작업이 필요합니다. 역시나 먼저 자유도를 구하는데, 쉽게 하기위해 그래프도 같이 그립시다. 그리고 이 그래프와 동일한 형태를 띄는 직교배열표에 매핑 합니다. 마찬가지로 남은 배치는 에러항 으로 구분합니다.

3.4. Dummy method

의수준법이라고도 불립니다. m수준의 인자를 n수준 열에 배치하고자 할때 n이 더 고차원이라면 배치가 가능합니다. 당연하겠죠. 2수준계가 3수준계 열에 들어가는 경우다 보니까, 경우의 수 몇 개를 지우는 행위거든요.
3.5. Compounding Factor Method

의수준법 으로도 줄이기 애매한 경우가 있습니다. A, B가 2수준, C, D, E가 3수준에 정직하게 한다면 3개의 열이 놀고 18번의 실험을 해야겠죠. 그런데 사실 자유도가 8인데 말입니다. 9번의 실험으로도 가능하지 않을까 싶습니다. 그래서 복합인자법 이 있습니다. 만약 2수준 A, B를 합친다면? 3수준의 경우가 나오겠네요. 그럼 위 우측 이미지처럼 9번의 경우에도 가능한 직교배열표가 나옵니다.
다만, 복합인자로 만들어진 두 인자 사이의 직교성이 없어집니다. 그렇지만 이들 인자 전체에 대해서는 직교성이 유지됩니다. 큰 문제 없다는 것이죠.

반대로 불필요한 경우에 대해 소거를 하여 수준계를 낮출 수 있습니다. 2수준계 인자 A, B 와 3수준계 인자 C,D,E,F,G,H,I 가 있습니다. 이러면 2개 / 7개를 자유도로 따져보면 2 + 21 = 23이 나오네요. 혼합형 직교배열을 쓴다면 L36에 배치를 해야합니다. 그러나 L36은 2수준계 11개, 3수준계 12개라 에러항이 많이 발생합니다. 제일 적은 실험횟수를 이용해야하는데 어찌보면 많은 낭비입니다. 그럼 A, B를 3수준계로 올리면 18의 자유도가 나오네요. 표준 3수준계 직교배열표 L27이 나오네요. 이는 3수준계 13개 얘기입니다. 이래도 낭비가 있네요. 사실 양보하는 방법이 있습니다. 3수준계 인자중에서 하나만 2수준계를 내려봅시다. 그리고 2수준계 A, B 중 하나를 복합인자로 합쳐봅시다.
저는 3수준계 인자 C를 선택하겠습니다. 그리고 A를 복합인자로 채택할게요. 그럼 A1C1, A2C1, A1C2인 3수준계 복합인자가 만들어집니다. 그러면 이제 2수준계 인자 A 한개와 3수준계 인자 7개가 나옵니다. 자유도는 15, L18(2^1 x 3^7) 혼합형 직교배열표를 쓸 수 있어서 기존에 채택하려 했던 L36에 비해 절반의 실험횟수가 나옵니다.
3.6. Examples
- 2수준계 인자 A, B, C, D에 교호작용은 AB, AC, BC
- 2수준계 인자 A, B, C 교호작용 AB 이 실험을 두개의 블록(R)로 나누자 한다.
- 2수준계 인자 A, 3수준계 인자 B, C, D

첫번째는 자유도가 7이며 L8(2^7)에 딱 맞춰서 적용가능합니다.
| 실험번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 8 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 기본표시 | a | b | ab | c | ac | bc | abc |
| 실험배치 | A | B | AB | C | AC | BC | D |
두번째는 자유도가 5이며 L8(2^7)의 선점도와 안맞지만, 선점도 변형에 의해 배치되지 않은 열에 대해서 주효과를 배치하면 됩니다.
| 실험번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 8 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 기본표시 | a | b | ab | c | ac | bc | abc |
| 실험배치 | A | B | AB | C | e | e | R |
2수준계 인자 A, 3수준계 인자 B, C, D는 의수준법으로 사용해봅시다. L9으로 구할 수 있고 아래와 같이 만들 수 있습니다.
| 실험번호 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | A1 | B1 | C1 | D1 |
| 2 | A1 | B2 | C2 | D2 |
| 3 | A1 | B3 | C3 | D3 |
| 4 | A2 | B1 | C2 | D3 |
| 5 | A2 | B2 | C3 | D1 |
| 6 | A2 | B3 | C1 | D2 |
| 7 | A1’ | B1 | C3 | D2 |
| 8 | A1’ | B2 | C1 | D3 |
| 9 | A1’ | B3 | C2 | D1 |
| 인자배치 | A | B | C | D |
