1. Sigma(σ)
σ(sigma)는 표준편차라고 얘기합니다. 여기서의 편차란 무엇일까요? 편차는 평균과의 차이를 얘기합니다. 표준을 앞에 붙이면 대표한다는 의미가 부여됩니다. 즉 표준편차, σ(sigma)는 편차들을 대표하는 값입니다.
그런데 사실 이렇게 말로하는 것과 계산식은 조금 다릅니다. 왜냐하면 데이터 규모를 설명할 땐 Variance(분산)을 말하기 때문인데요. 분산은 편차간 부호를 없애기 위해서 제곱이 들어가고 표준편차는 그 분산에서 제곱을 제거합니다. 아래 그림으로 분산을 통한 편차에 대해 얘기하겠습니다.
1.1. Gen sample

-1에서 1까지 균일한 확률로 샘플을 만들었습니다. 이 점들이 얼마나 밀집됐는지 보는 것이 분산과 표준편차입니다. 누가보면 대충 적당히 떨어져있네라고 할 것이고 누군가는 어차피 -1~1까지 모여있으니 큰 수로보면 좁을거야라고 얘기할 것입니다. 그렇다면 객관성을 가지기위해서는 수치로서 얘기를 해보려 합니다.
1.2. Put Average point

먼저 이 점들을 대표하는 점을 하나 찍었습니다. 지금 뿌려진 점들의 가장 중앙을 찍는다는 것은 점의 x위치와 y위치의 평균이라고 볼 수 있습니다. 우리의 주제는 이 점들이 얼마나 밀집됐는지를 보는 것이기에 이 중앙점과 얼마나 많이 벗어나있는 지, 거리를 재보겠습니다. 거리는 대각선으로 잴 것이구요. 대각선을 구하는 방법은 피타고라스의 정리를 이용하여 잴 것입니다.
1.3. Calculate distance

막상 그려보긴 했는데 이 거리를 일렬로 세워서 크고 작음을 비교할 필요가 있겠네요. 거리에 대해서 bar plot(막대그래프)으로 바꿔보겠습니다.

이렇게보니 중앙점과 가깝기도 하고 멀기도 하고 적당한 애도 있고 고루고루 있어 보입니다. 지금 저는 굉장히 주관적인 판단을 했습니다. 저희 주제는 객관성을 가진 밀집도를 봐야하니깐, 이 중앙점간의 거리들의 평균을 구해봅시다. 거리는 편차일테고 평균을 구한다는 것은 대표한다는 의미도 되니까 표준편차라고 할 수 있을까요?
안타깝게도 아닙니다. 방금 위 가정은 평균절대편차라고 부릅니다. 직관적이죠? 그렇다면 표준편차에 대한 표준의 접근을 해봅시다. 평균값에 대해 편차의 제곱의 합이 최소가 된다는 사실이 있습니다. 이를 가장 잘 이용한 것이 현재 최적화와 인공지능분야에 많이 사용되고 있는 최소제곱법입니다. 평균값에 대한 편차를 제곱하면 우리가 구했던 샘플들의 평균 간의 거리, 그 거리와 거리 평균간의 차이, 그리고 그 구한 차이의 효과를 극명하게 제곱을 한다면?
역시 그림으로 보는게 훨 낫습니다.
1.4. Calculate difference distance from mean

거리간의 평균을 구하여 차이를 빨간선으로 그어 놨습니다. 그런데 여기서 제곱을 하는 이유가 있을까요? 사실 제곱을 하면 차이가 적게 나면 더 적어지고 차이가 크게나면 더 크게납니다. 차이에 대해서 확실하게 차이를 두겠다는 의미입니다.
1.5. Squared values

아까 위에있던 빨간선(차이)를 제곱하여 box plot으로 만들었더니 크게 차이났던 값은 더 커지고 작은 차이는 더 작아졌습니다. 이제 이 값들의 평균을 구하면 분산이 됩니다. 분산이 제곱하여 얻어진 결과이기에 제곱을 루트로 걷어내면 표준편차가 됩니다.
1.6. Conclusion

CalcVar(직접 계산한 분산), CalcStd(직접 계산한 표준편차), absVar(절대평균편차_변수명의 ‘Var’은 제가 실수했습니다.), RealVar(MATLAB함수로 가져온 분산), RealStd(MATLAB함수로 가져온 표준편차)
마지막으로 정리하겠습니다. 저희는 Sample이 객관적으로 얼마나 밀집됐는 지를 확인하고자 했습니다. 그리고 그 과정에서 평균간의 차이에 제곱을 하면 더 드라마틱한 효과를 볼 수 있었으며 이 극적인 숫자들의 평균이 분산이었고 제곱을 제거하면 표준편차(σ, sigma)가 됐습니다.
2. 6-Sigma
σ(sigma)에 대해서는 알았는데, 6-Sigma란 무엇일까요? 수리적으로는 양측 3*표준편차의 범위를 의미합니다. 그런데 이게 품질과 무슨 관련이 있을까싶죠. 품질에 대해서 조금 얘기를 하고 이어서 설명하겠습니다.
2.1. Quality
품질에 대해서 얘기하자면 좋은 품질은 좋은 성능을 내는 것이냐 물어보면 맞다고는 하지만 찝찝한 느낌이 있습니다. 진정한 좋은 품질은 신뢰성과 연결지어야 합니다. 그래서 늘 비슷한 성늘을 내는 것이 맞겠죠. 그렇다면 고장도 잘 안나고 어느 환경적인 영향도 덜 받는 것이 좋습니다. 반대로 불량품이란 요구한 성능에 미달하는 것도 불량품이고 요구한 성능에 과적합하는 것도 불량품일 수 있습니다.
예를들어 자동문을 만들었구요. 문이 열렸을 때 가운데에 물체를 놔두겠습니다. 30의 부하를 받으면 닫히다가 다시 열어야되는 조건으로 40,000개의 자동문을 검사하겠습니다. 생산라인에서 나온 제품은 대체적으로 균일한 성능과 성질을 가집니다. 다시 언급하지만 불량품이란 그 균일한 성능과 성질에서 벗어난 경우를 의미합니다. 각설하고 자동문 데이터는 아래와 같은 그래프로 보여줄 수 있습니다. 물론 실제 데이터는 아닙니다.

2.2. Background
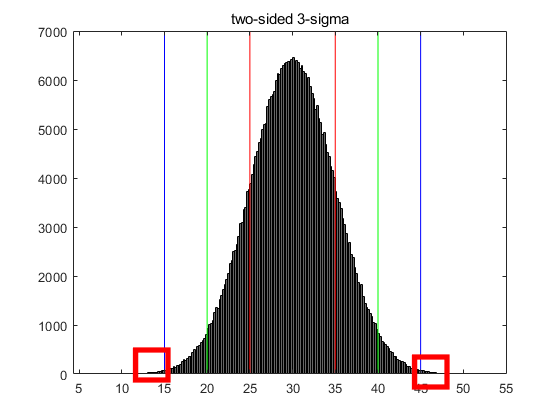
여기서 더 나아가 양측 3 * 표준편차를 그려보겠습니다. 적색이 1 * 표준편차, 녹색이 2 * 표준편차, 청색이 3 * 표준편차 입니다.

위의 굵은 적색 네모박스보이시나요? 얘네는 30의 부하를 받으면 문을 다시 열라고 했는데, 15의 부하도 안돼서 문을 열었거나(좌측) 45의 부하를 받았음에도 문을 닫은 경우(우측)입니다. 좌측의 경우는 적은 부하로 인하여 오작동할 확률이 크고, 우측의 경우는 인체위협 가능성이 있습니다. 둘 다 불량품입니다.
2.3. Principle
근데 왜 굳이 양측 3 * 표준편차로 했을까요? 왜 3일까.. 2로 하면 더 좋은 품질의 제품으로 걸러낼텐데 말이죠. 아래의 수리적인 설명으로 말씀드리겠습니다.
아주 쉽게 얘기하면 전체 제품들의 평균(u)가 계산한 분산만큼 정규분포속에 퍼져있다는 조건을 둡니다. 가정을 하는 것이기에 실제 데이터에선 정규성 검정을 해야합니다. 그렇다면 아래와 같이 표준화를 진행할 수 있습니다.
예시로 들었던 자동문은 평균(u) 30에 표준편차(σ) 5라고 했다면, 표준화를 통해서 평균(u) 0에 표준편차(σ) 1로 바뀌었습니다. 그러면 3*σ = 3이겠죠?
표준정규분포 P{Z>3} = 0.00135입니다. 정규분포는 대칭이니까 -3도 0.00135입니다. 즉, 아래와 같은 식이 성립되죠.
\[\begin{array}{l} P\{\ -3\leq\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\leq3\}=1-(0.00135*2)=0.9973 \end{array}\\\]지금까지 X bar에 대해서 얘기하지 않았습니다. 이제 말씀드리면 X bar는 추출한 검사 샘플의 평균을 의미합니다. 예로 들었던 자동문 검사 샘플 평균이죠. 위 수식이 얘기하는 내용은 Sample의 평균(X bar)이 자동문 제품 자체의 표준편차(σ) 양측 3안에 있을 확률이 99.73%를 의미합니다. 그 외를 벗어난다면? 샘플이지만 자동문 제품 자체의 평균(u)이 아니라고 볼 수 있죠.
2.4. Control chart
현실적으로 생각해보면 위 이론은 얘기가 달라집니다. 샘플 1000개를 테스트했는데, 2개 불량이 났으면, 이 두 개가 0.27%의 영역에 들어왔구나 나름 납득이 됩니다. 근데 1000개를 테스트 했는데 60개 불량이 났으면, 전체 제품의 0.27% 영역에 있는 불량품들 중에서 60개 불량을 고작 1000개 가지고 검출해냈으면 역사적인 순간이겠죠. 최소의 검사 샘플로 다량의 불량을 검출해냈으니까요. 그러나 승리자의 성취감보다는 찝찝함이 남아있습니다. 실제로 그럴리가 없거든요.
그래서 생각합니다. 0.27%가 실현되기 어려운 확률이니, 이것은 공정의 평균이 변했구나. 제품자체의 평균이 변했구나로 생각하게 됩니다. 그렇다면 이 제품의 변동을 관리할려면 어떻게 해야할지 고민하게 되면서 Control chart(관리도)가 나오게 됩니다. 관리도는 다음 포스팅에서 진행합니다.
