1. Principal Component Analysis Theory
1.1. Useful properties for variables
주성분분석(PCA)는 차원축소의 한 기법으로 Uncorrelated(무관계성)와 Explicability(설명력)가 중심입니다.
1.1.1. Uncorrelated

다중공선성(Multicollinearity)이랑 연관있습니다. 데이터에서 존재하는 컬럼들은 차원(Dimensions)라고 얘기를 합니다. 차원이라고 얘기하는 데에는 그만큼 다른 컬럼간 영향 혹은 관계없이 독립적인 존재로서 의미가 있다는 것이죠. 그러나 다른 변수들 간에 상관관계가 높으면 Multicollinearity가 존재하여 데이터 분석의 의미가 없어집니다. 좀 더 학술적으로 얘기하면 OLS회귀계수 추정과 검정이 무의미해집니다.
1.1.2. Explicability

세상 모든 변수는 대부분 다른 변수와 상관관계를 지니고 있습니다. 두 개 혹은 그 이상의 변수끼리 상관관계가 매우 높다면, 이 중에서 하나만 사용해도 충분한 설명이 되겠죠. 예를 들어 나이와 주름에 대해서 얘기해봅시다. 나이가 들수록 주름은 늘어납니다. 그러나 주름이 많다고해서 무조건 나이가 많다고 보기엔 살짝 어려움이 있죠. 이런 경우는 나이가 설명력이 높다고 얘기할 수 있습니다. 아래 그래프처럼 Var(Age), 나이의 분산이 주름보다 더 넓게 분포되어 있음을 볼 수 있습니다.

1.2. Geometric approach


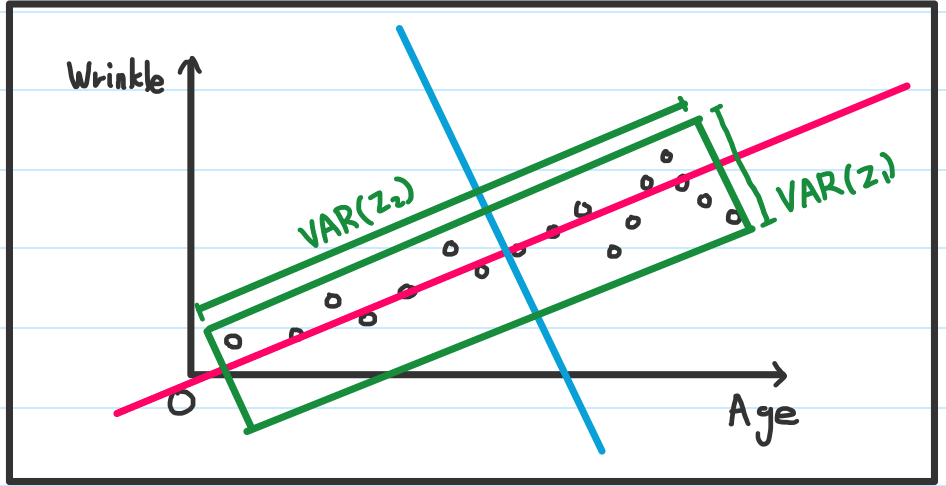
그렇다면 형상적으로 혹은 기하학적으로 PCA에 접근해봅시다. 위 그래프처럼 나이를 x축으로 두고 주름을 y축으로 두겠습니다. 나이가 많으면 주름도 많고, 나이가 적으면 주름도 적습니다. 그러니 PCA에서 중요한 Uncorrelated와 Explicability를 직접 해봅시다. 첫번째로 Uncorrelated, 즉 나이와 주름간의 우측 위로 올라가는 상관관계를 제거해봅시다.
1.2.1. 상관관계 제거

첫번째로 할 작업은 저 분포들 사이를 꿰뚫는 선을 그립니다. 적색선이 만들어지구요. 이 적색선을 직교하는 파란선을 그립니다.

이제 적색선을 x축으로 파란선을 y축으로 두고 그래프를 다시 만들어보니 서로 상관관계가 강할때 보이는 대각선 형태의 분포가 사라지게 됩니다.
1.2.2. 높은 설명력

처음 작업했을 당시 데이터 분포는 나이가 많음을 볼 수 있습니다. 이는 나이가 높은 설명력을 가지고 있고, 상관관계 제거를 통해서도 여전히 적용됩니다.

이제 적색선을 x축으로 파란선을 y축으로 두고 그래프를 다시 만들었을 때 녹색영역이 데이터 분포 영역입니다. 이때 Var(z1)이 Var(z2)을 비교했을 때 z1이 설명력이 높다고 볼 수 있습니다. 참고로 그래프 축을 회전하는 것은 선형변환이라고 합니다.
1.3. Process
기하학적으로 어떻게 상관관계가 제거되고 어떤 변수가 설명력이 높은 지 확인할 수 있었습니다. 이번엔 선형변환을 통해서 이뤄지는 작업을 수리적으로 풀어보겠습니다. 단 선형대수학에 대한 정보없이는 알기 어려우니, 기하학적 접근을 이해하셨다면 넘어가셔도 됩니다.
먼저 선형변환을 수식으로 얘기하면 아래와 같습니다.
\[\begin{aligned} x_1\qquad ->\qquad z_1 = e_{11}x_1 + e_{12}x_2 \\ x_2\qquad ->\qquad z_2 = e_{21}x_1 + e_{22}x_2 \\ Var(x_1, x_2) \, \neq 0 \qquad -> \qquad Var(z_1, z_2) \, = 0 \end{aligned}\]이제 본격적으로 PCA를 진행하겠습니다. 데이터 행렬 X가 있다고 가정합니다. 위의 선형 결합에 대해서 수식을 적용하면 공분산 행렬의 고유 값-고유 벡터 쌍을 계산하여 얻어짐을 표현할 수 있습니다.
이때 얻어지는 z는 주성분이라 부르며 수식과 선형시스템이 모두 p로 끝나는 것처럼 정방행렬로 만들어진다. 이제 여기서부터는 가장 큰 람다를 기준으로 z를 몇 개를 선택하는 지(주성분 선택)와 그 선택된 주성분이 무엇을 의미하는 지 명명(labeling)하는 작업은 아주 중요하지만 주관적이기에 실습에서 보여드리겠습니다. 이 밑으로는 임의의 데이터를 이용해서 Eigen vector를 얻어 임의의 PCA를 진행합니다.
1.4. PCA practice
제가 지금부터 생각나는 숫자를 마음대로 불러보겠습니다. 단 갈수록 높아지는 게 조건으로요. 그게 곧 데이터가 될 것입니다.
데이터 생성
공분산 행렬 구하기
공분산 행렬의 Eigen value 구하기
Eigen value 계산
선형시스템 구성
고유 벡터e1에 X를 투영
고유 벡터e2에 X를 투영
기존 값과 바뀐 z값 비교

2. Implement
2.1. Heart disease
실습에 사용할 데이터는 Kaggle Hear Disease UCI에서 구했습니다. 해당글 내용에 따르면, 76개의 속성이 있으나 공식적인 실험은 76개의 속성들 중에서 14개의 부분집합으로 사용했다고 합니다. Goal이라는 필드가 심장병이 있음을 나타내고 0~4의 범위를 지닙니다.
그러나 저희는 PCA가 목적이기 때문에 네이밍 작업 전까지, 위 내용은 크게 상관없습니다. 이 글의 실질적인 핵심은 14개의 속성의 상관관계가 있는 지 알아보고, PCA를 진행하여 상관관계가 높아서 생기ㅇ는 Multicollinearity를 제거하는 것이 목표입니다. 또한 PCA를 진행하면서, 주요한 네가지를 얘기하려고 합니다.
1. 표준화를 진행하여 변수간 스케일을 동일하게 할 것
2. 85% 이상의 설명력을 가지도록 주성분을 채택할 것
3. Eigen Value값이 1이 넘는 주성분을 채택할 것
4. 채택된 주성분은 논란의 여지가 최소화된 네이밍을 사용할 것
이 내용을 중점으로 아래 코드를 설명하겠습니다.
2.2. MATLAB code description
MATLAB 복사하기 쉽게된 전문은 제일 아래에 있습니다. 지금부터는 설명입니다.
1
2
3
clc, clear
Medical_DataSet = readtable('Data\heart.csv');
NormCandidate = [1 0 1 1 1 0 0 1 0 1 1 1 1 0];
Kaggle Hear Disease UCI에서 데이터를 가져왔습니다. 변수를 초기화한 다음, 데이터를 불러옵니다. 그리고 아래 설명에 따라 표준화를 진행할 설명변수 자리에 1을 표기했습니다.
표준화
표준화를 할 변수를 14개 중에서 골라봅시다. 표준화 대상인 변수는 파랑 굵음으로 표현하겠습니다. 굳이 할 필요 없는데 확실하게 하고자 표준화하는 변수는 파랑 일반으로 표현하겠습니다. 변수에 대한 설명은 Kaggle Hear Disease UCI에 나와있는 그대로 가져왔습니다.
- age
- sex(1-male, 0=female)
- chest pain type (4 values)
- resting blood pressure
- serum cholestoral in mg/dl
- fasting blood sugar > 120 mg/dl
- resting electrocardiographic results (values 0,1,2)
- maximum heart rate achieved
- exercise induced angina
- oldpeak = ST depression induced by exercise relative to rest
- the slope of the peak exercise ST segment
- number of major vessels (0-3) colored by flourosopy
- thal: 3 = normal; 6 = fixed defect; 7 = reversable defect
- target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
arr_DataSet = table2array(Medical_DataSet);
%Before normalize
figure
hold on
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
plot(arr_DataSet(:,i))
end
end
hold off
%normalize
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
arr_DataSet(:, i) = ((arr_DataSet(:, i) - min(arr_DataSet(:,i))) / (max(arr_DataSet(:,i)) - min(arr_DataSet(:,i))));
end
end
%After normalize
figure
hold on
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
plot(arr_DataSet(:,i))
end
end
hold off
가져온 table을 수치적으로 처리하기 쉽게 array의 자료형으로 변환합니다. 표준화를 진행하면 아래 그래프처럼 0과 1사이의 값으로 변경됩니다.


상관관계 분석
여기서부터 제가 가져온 데이터가 PCA를 실습하기에는 올바르지 않다는 걸 느꼈습니다. 왜냐하면 이미 설명변수간의 상관성이 낮은 편이더라구요.(보통 0.6 이하) PCA의 목적은 차원축소를 통해 뒤에 진행하는 연산을 간소화하는 것도 있지만 각 설명변수간의 상관성을 낮춰 Multicollinearity를 없애는 이유기도 했습니다.
그러니 이번 데이터를 통해 얻을 수 있는 것은 변수를 줄일 수 있다입니다.
1
2
3
%correlation matrix
data_corr = corr(arr_DataSet);
figure, imagesc(data_corr), colorbar

PCA
1
2
3
4
5
6
7
8
9
%PCA
[coeff, score, latent, tsquared, explained] = pca(arr_DataSet);
checker = 0;
for PCs=1:height(Medical_DataSet)
checker = checker + explained(PCs);
if(checker > 88)
break;
end
end
PCA를 진행했고, 설명력이 88%가 넘어가는 주성분까지를 선정했습니다. (7개) 이미 데이터가 깔끔해서 주성분이 많이 나오는데 보편적으로는 3~4개쯤에 설명력 85%를 넘깁니다. 그리고 이미 잘 독립된 형태의 데이터라 그런지 고유값 또한 1을 넘는 것이 안 나오네요.

coeff는 주성분 계수, score는 주성분에 대한 점수, latent는 Eigen vlaue입니다. tsquared는 본 글에서 사용하지 않았으니 넘어가고 explained는 주성분의 데이터 설명력입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
%Visualization
cumplot = cumsum(explained);
limline = cumplot.*0 + 88;
figure
hold on
plot(limline, 'red');
plot(cumplot, '--blue');
hold off
latent(find(latent > 1.0))
coeff(:, PCs+1:width(Medical_DataSet)) = [];
arr_DataSet = arr_DataSet * coeff;
PCAMatrix = arr_DataSet(:, 1:PCs);
pca_corr = corr(PCAMatrix);
figure, imagesc(pca_corr), colorbar
이번 PCA 시각화 자료입니다. 88%를 기준으로 누적 데이터설명률을 표현하고,
1.0 이상의 Eigen value를 가지는 주성분을 출력하며 선형변환 후 설명변수간의 상관행렬을 확인합니다.

2.3. MATLAB code 전문
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
clc, clear
Medical_DataSet = readtable('Data\heart.csv');
NormCandidate = [1 0 1 1 1 0 0 1 0 1 1 1 1 0];
arr_DataSet = table2array(Medical_DataSet);
%Before normalize
figure
hold on
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
plot(arr_DataSet(:,i))
end
end
hold off
%normalize
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
arr_DataSet(:, i) = ((arr_DataSet(:, i) - min(arr_DataSet(:,i))) / (max(arr_DataSet(:,i)) - min(arr_DataSet(:,i))));
end
end
%After normalize
figure
hold on
for i=1:width(Medical_DataSet)
if NormCandidate(i) == 1
plot(arr_DataSet(:,i))
end
end
hold off
%correlation matrix
data_corr = corr(arr_DataSet);
figure, imagesc(data_corr), colorbar
%PCA
[coeff, score, latent, tsquared, explained] = pca(arr_DataSet);
checker = 0;
for PCs=1:height(Medical_DataSet)
checker = checker + explained(PCs);
if(checker > 88)
break;
end
end
%Visualization
cumplot = cumsum(explained);
limline = cumplot.*0 + 88;
figure
hold on
plot(limline, 'red');
plot(cumplot, '--blue');
hold off
latent(find(latent > 1.0))
coeff(:, PCs+1:width(Medical_DataSet)) = [];
arr_DataSet = arr_DataSet * coeff;
PCAMatrix = arr_DataSet(:, 1:PCs);
pca_corr = corr(PCAMatrix);
figure, imagesc(pca_corr), colorbar
