1. About the search
1.1. Tree, Graph
Search를 얘기하기 전에 Tree와 Graph에 대해서 먼저 설명합니다. 두 차이를 안다면 넘어가십시오.
1.1.1. Tree

소프트웨어에서 얘기하는 Tree는 실제 나무와 반대의 모양을 띄고 있습니다. 제일 위에를 Root라고 얘기하며 Root는 한 개입니다. 여러분들이 Tree를 받아들이기 위해서는 자료구조라는 점에 주목해야됩니다. 보통 알고리즘과 자료구조를 같이 이야기합니다. 자료구조는 세상에 널리 알려진 구조들을 Data에 접목시켜 어떤 형태를 띄는 것입니다. 그래서 대부분 자체적인 기능을 하지 않습니다.

물론 Tree에는 여러가지 종류가 있으나 자료구조에 대한 포스팅 기회가 온다면 그 때 말씀드리겠습니다. Tree는 자료구조이며 얘가 어떤 알고리즘으로서 무언가를 해결하고 동작하지 않습니다. 이번 MATLAB, 탐색 알고리즘의 내용은 이 Tree안에서 여기저기 찾아 다닐 것 입니다.

1.1.2. Graph

사실 저희가 이용할 자료구조는 Graph입니다. 단언컨데 우리가 탐색 이용할 대부분의 자료구조는 Graph입니다. 왜냐하면 세상 알려진 문제들의 대부분은 Graph의 성질을 지니고 있죠. 여기서 Tree와 Graph에 대해 얘기하자면 Tree에서 순환하는 성질이 발견되면 Graph가 됩니다. 우연히 새로운 길에서 길을 잃었을 때, 왔던 길에 다시 되돌아 올 수 있습니다. 빠져나갈 길을 탐색하는 과정에서 순환이 일어난 것이죠. 그런 경험들을 자료구조로 변경하면 Graph가 됩니다.
1.2. Uninformed Search
Uninforemd Search는 미리 정의되지 않은 구간에 대해 탐색함을 의미합니다. 대표적인 예는 미로찾기입니다. 미로에 입장하자마자 지형에 대해서 알 수도 없으며 무작위로 이동하게 됩니다. 이러한 Uninformed search에는 대표적으로 Breadth First Search와 Depth First Search로 나뉩니다. 이름 그대로 BFS는 좌우로 움직이며 탐색하고 DFS는 아래 위로 훑으며 탐색합니다. DFS와BFS를 근본으로 둔 여러 탐색 알고리즘들은 나중에 설명하도록 하겠습니다.
1.2.1. Tree 와 Search
1.1은 자료구조에 대해 설명드렸습니다. 1.2는 알고리즘에 대해 설명드렸구요. 본문에 진행하는 식인종 문제를 하기에 앞서서 두 가지 간략한 설명이 필요했습니다. 이제 왜 설명이 필요했었는 지 말씀을 드리겠습니다. Problem-Solving에는 주로 Optimization(최적화), AI(인공지능)라는 키워드가 들어갑니다. 이번에 진행하는 식인종 문제는 Optimization에 해당된다고 볼 수 있습니다.
대부분의 Optimization의 문제들은 경우의 수와 반복에 대해 주 토픽으로 다룹니다. 1.1에서 얘기한 Tree는 Optimization에 나온 문제의 경우의 수와 반복된 상태들을 모두 담고 있습니다. 예를 들어서 주사위를 네번 던진다고 해봅시다. 그렇다면 제가 주사위를 던지기 전에는 1~6까지의 숫자가 나옴을 인지하고 있습니다. Tree도 마찬가지로 한번 밑으로 진행할 때 많아 봤자 6개의 가지가 만들어 지겠죠. 이렇게 만들어진 경우의 수를 Child node라고 부릅니다. 그렇다면 제가 숫자 4가 나올때 까지 계속 주사위를 굴린다면? 언제 성공할까요?
사실 장담할 수 없습니다만, Uninformed Search에서는 더 더욱 장담할 수 없습니다. 주사위를 0.1초에 한번씩 던질껀데 계속 1만 나오면 어쩔래? 라는 가정이 있거든요. 그렇다면 Tree의 깊이는 한도 끝도 없이 무한한 상태에 이릅니다. 자, 여러분은 알게 모르게 Tree의 특징을 익혔습니다. 바로 경우의 수는 Child node의 수를 결정하고 반복 수는 Tree의 깊이, Level을 결정한다는 것이죠.
1.2.2. DFS 와 BFS
DFS는 Root node에서 시작해서 아래위로 훑고 지나다니는 탐색 기법입니다. 방금 처럼 Tree의 node가 무한한 상태에 빠진다면? DFS는 돌아오지 못할 것입니다. 주사위를 예로 들었는데 현실에서 숫자 4는 넉넉하게 30번만 던져도 찾을 수 있습니다.
BFS는 Root node에서 좌우로 돌아다니기에 다음 만들어진 Child node를 모두 방문하고 나서야 다음 Level로 넘어간다는 점이 있습니다. 그렇다면 일상적인 넉넉 30 Level안에 4를 찾을 수 있겠죠? 이처럼 BFS는 DFS에 비하여 Node안에 들어있는 답을 반드시 찾아냅니다.
2. Missionary-Cannibal problem
2.1. Introduction


UnInformed search에 대표적인 식인종 문제입니다. 식인종과 선교사를 모두 배를 태워 강을 건너야합니다. 허나 배에 탈 수 있는 인원은 정해져있죠. 또한 추가적인 규칙이 있습니다.

식인종과 선교사의 인원이 동등하다면, 그 어떤 사건사고가 발생하지 않습니다. 아주 평화롭고 식인종은 입맛을 다시고 있습니다. 그러나

선교사의 인원이 식인종보다 적어지면 식인종은 본 모습을 드러내기 시작합니다. 선교사를 잡아먹어 모두 배를 건널 수 없습니다.
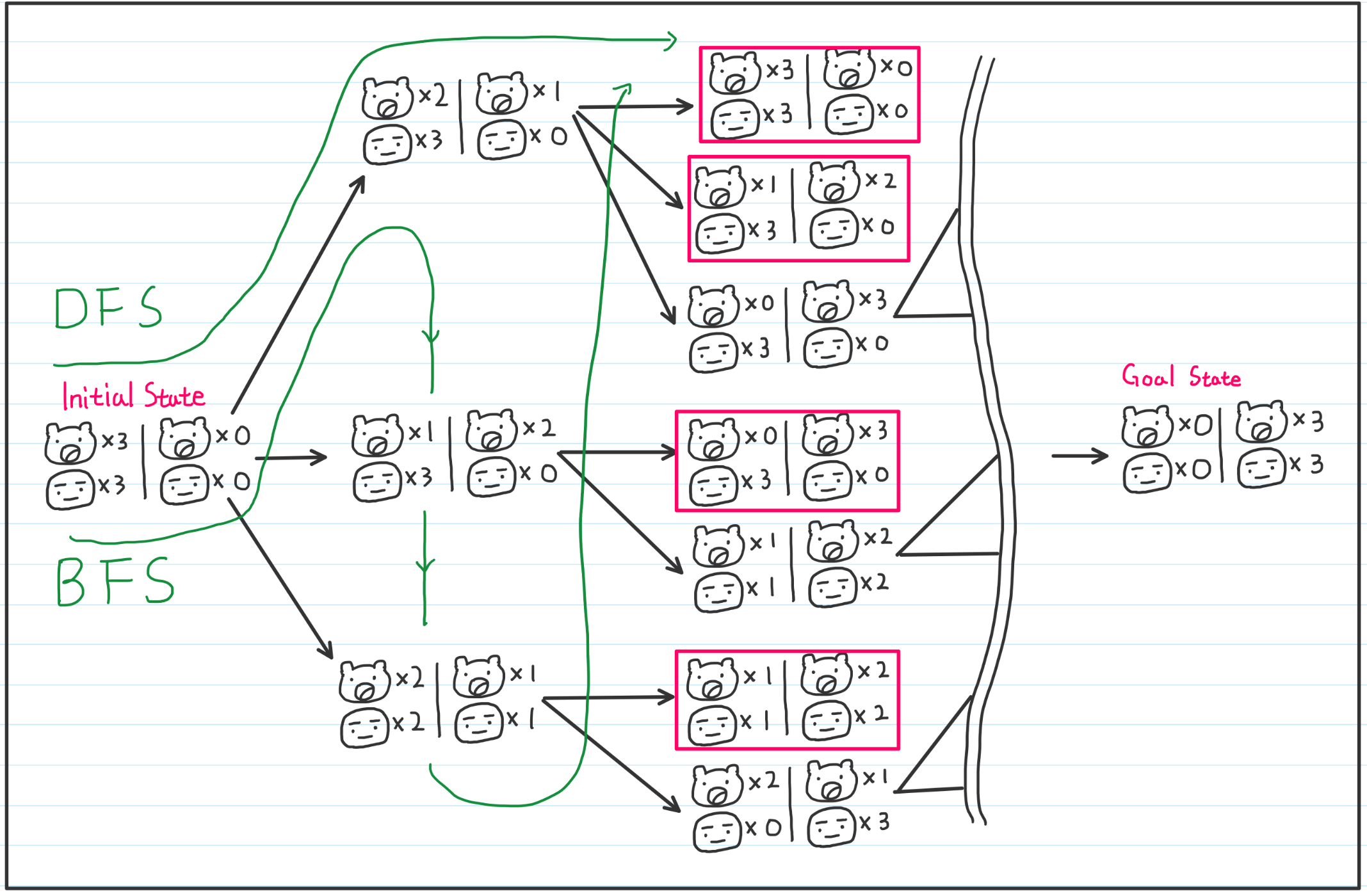
2.2. State space

우리가 해결할 문제에 대한 상황을 어느정도 트리로 구현해봤습니다. 제일 좌측이 Root node이며 시작상태, Initial state라고 합니다. Feasible solution에 대해서 간단하게 그려봤습니다.
3. Implement

이제 MATLAB을 이용하여 본격적인 구현을 할 건데요. 먼저 기본적인 식인종 문제를 하면 재미없어서 조금 응용을 해봤습니다.

식인종과 선교사를 각 30명씩 만들었구요. 배는 최대 5명을 실을 수 있습니다. 앞서 말했듯 Child node의 수를 앞으로 생길 경우의 수라고 보겠습니다. 그렇다면 최대 5명을 태울 수 있는 경우의 수는 235입니다. 수식은 아래와 같습니다. 그리고 Tree Depth를 결정하는 최대 반복 수는 제법 많겠죠?
그래서 제가 미리 돌려봤습니다. 단순히 BFS(Breadth First Search)로 했을 때는 41061번째에 모두 옮기더라구요.

3.1. Depth-Limited Search
기왕 실습하는 거 DFS(Depth First Search)와 BFS(Breadth First Search)를 섞어서 사용해볼까요? Tree의 깊이가 10까지는 DFS로 탐색하다가 그 뒤부터는 BFS로 탐색하도록 하겠습니다! 결과를 먼저 알려드릴께요. 이번 소스에서는 큰 차이가 있으나, 일반적으로는 큰 차이 없습니다! 이유는 학습되지 않은 Depth때문입니다. 만약 보편적인 정답이 어느정도 깊이에 있었는 지 대충 알 수 있다면 효과가 있었겠죠? 그러나 Uninformed Search의 특성상 한번 답을 찾았으면 더 할 필요 없습니다. 이정도의 호기심만 놔두고 Depth Limited Search에 대해서 설명하겠습니다.

Depth Limited Search는 특정 깊이까지는 DFS로, 그 다음부터는 BFS로 진행하는 Algorithm입니다. 깊이를 정한다는 점이 매우 흥미로운데 사실 Complete하지도 Optimal하지도 않습니다. 심지어 일반적인 BFS보다 크게 경쟁성이 없습니다. 다만, 깊이를 설정함에 따라 보편적으로 BFS보다 빠르며 공간복잡도 또한 BFS보다 낫습니다. 그럼에도 불구하고 이번 실습을 DLS로 알려드리는 이유는 깊이제한을 0으로 설정하면 그냥 BFS로, 아주 높은 값으로 설정하면 DFS로 사용할 수 있기 때문이죠.
3.2. MATLAB code 설명
30명에 5인승 배 규모의 식인종 문제를 DLS, 깊이제한탐색을 이용하여 해결합니다. MATLAB으로 구현했으며, MATLAB 복사하기 쉽게된 전문은 제일 아래에 있습니다. 지금부터는 설명입니다.
1
2
clear, clc
import java.util.LinkedList
모든 변수를 초기화시켜줍니다. DLS를 사용하기 위해서 양쪽 방향으로 push,pop가능한 java의 LinkedList를 불러옵니다.
1
2
3
4
5
6
7
8
9
10
11
12
%Configuration parameters
Steps = 1;
VectorSize = 30;
Passenger_boat = 5;
Level = 0;
DepthLim = 10;
%Initial State
InitState = [VectorSize 0 Level; VectorSize 0 Level];
%Goal State
GoalState = [0 VectorSize Level; 0 VectorSize Level];
StateSpace = LinkedList();
StateSpace.addLast(InitState)
몇 번 반복했는 지 알기위한 Steps와 식인종, 선교사의 인원은 VectorSize로 결정합니다. Passenger_boat는 보트 최대 탑승원 수, Level은 Node가 현재 Tree에서 어느정도 Depth를 가지고 있는 지 알아보기 위함입니다. DepthLim은 DLS의 중요요소인 깊이 제한을 담당합니다. 현재는 Depth가 10을 넘었을 때 BFS를 하도록 설정했습니다.
최초의 상태는 강 좌측으로 모두 30명이 있으며 1열-강 왼쪽 2열-강 우측 3열-노드의 레벨입니다. StateSpace에 처음 상태를 집어넣습니다.
1
2
3
4
5
6
7
8
Run = 1;
while(Run)
%Visit->
Visit = StateSpace.removeFirst();
if rem(Steps, 50) == 0
disp(['-' num2str(Steps) '-'])
Visit
end
시작입니다. BFS(Queue)는 First-In-First-Out, DFS(Stack)는 Last-In-First-Out입니다. 결론은 모두 removeFirst입니다. MATLAB의 화면표시는 Steps가 50단위로 나뉘어질 때 표기합니다.
1
2
3
4
5
6
7
8
CheckSum = Visit == GoalState;
if(sum(sum(CheckSum)) == 4)
'Goal State Found ->'
Steps
Visit
Run = 0;
break;
end
두번째는 GoalState와 비교입니다. 결론적으로 행렬 속 6개의 요소 중에 4개가 식인종, 선교사의 배치와 관련있습니다. Level을 담당하는 요소와 같을 수 있을까요? 절대 없는 경우로 만들었습니다. Level이 0일 때, 절대로 Goal state와 동일한 상태가 될 수 없기에 Goal state의 Level은 0입니다.
1
2
3
4
5
6
7
8
9
10
11
12
TempQ = GenChildNodes(Visit, Passenger_boat, VectorSize);
for i=1:TempQ.size
Containers = TempQ.removeFirst();
if Containers(1, 3) > DepthLim
StateSpace.addLast(Containers);
else
StateSpace.addFirst(Containers);
end
end
Steps = Steps + 1;
빼낸 node를 통해 Child node를 만듭니다. 만들어진 Child node의 Level이 DepthLim보다 크면, BFS(Queue)로 동작하기 위해 addLast를 합니다. 왜냐하면 node를 뺄 때, removeFirst를 하니까, 가장 최근에 들어온 node는 마지막에 빠져야 합니다.
반대로 Level이 DepthLim보다 작으면 DFS(Stack)으로 동작하기 위해 addFirst를 합니다. 마찬가지로 node를 뺄 때, 최근 것이 먼저 빠져야하기 때문입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
function y = GenChildNodes(InState, boatLim, VectorSize)
y = LinkedList();
%보트 인원
for cnt=1:boatLim
%Missionary
for cntsub=1:cnt
Temp = InState;
MNumber = Temp(1, 1);
if MNumber >= cntsub
RightNum = Temp(1, 2);
RightNum = RightNum + cntsub;
Temp(1, 2) = RightNum;
Temp(1, 1) = VectorSize - RightNum;
GenChildNodes에 대해서 알아봅시다. boatLim이 5인승이니까, Missionary-선교사 1명부터 탈 수 있는 경우, 5명 전부 탈 수 있는 경우의 모든 경우의 수를 넣어봅니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
CNumber = Temp(2, 1);
if CNumber >= cnt - cntsub
RightNum = Temp(2, 2);
RightNum = RightNum + (cnt - cntsub);
Temp(2, 2) = RightNum;
Temp(2, 1) = VectorSize - RightNum;
if feasibleSol(Temp)
Temp(:, 3) = Temp(:, 3) + 1;
y.addLast(Temp)
end
end
end
end
end
4명이 탈 차례인데 3명의 Missionary-선교사를 보냈다면 마저 1명의 Cannibal-식인종을 태워 feasibleSol함수에 점검합니다. 이동해도 문제없다고 한다면 가능해라고 판단하여 예비 Child node인 y에에 넣어줍니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
%Cannibal
Temp = InState;
Number = Temp(2, 1);
if Number >= cnt
RightNum = Temp(2, 2);
RightNum = RightNum + cnt;
Temp(2, 2) = RightNum;
Temp(2, 1) = VectorSize - RightNum;
if feasibleSol(Temp)
Temp(:, 3) = Temp(:, 3) + 1;
y.addLast(Temp)
end
end
end
중복의 경우의 수가 제거된 후 Cannibal만 이동하는 경우입니다. 메커니즘은 위 섹션과 동일합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function y = feasibleSol(ValidState)
%1행 - 선교사 2행 - 식인종
Missionary = ValidState(1, :);
Cannibal = ValidState(2, :);
CheckSum = Cannibal > Missionary;
if sum(CheckSum) == 0
y = true;
else
if Missionary(CheckSum) == 0
y = true;
else
y = false;
end
end
end
마지막으로 feasibleSol함수입니다. 현재 Cannibal과 Missionary 조합이 가능한지 불가능한지 알아봅니다. Cannibal이 Missionary보다 많은 상황이 있다면 false 그게 아니라면 가능한 상황이기에 true를 보냅니다.
3.3. MATLAB code 전문
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
clear, clc
import java.util.LinkedList
%Configuration parameters
Steps = 1;
VectorSize = 30;
Passenger_boat = 5;
Level = 0;
DepthLim = 10;
%Initial State
InitState = [VectorSize 0 Level; VectorSize 0 Level];
%Goal State
GoalState = [0 VectorSize Level; 0 VectorSize Level];
StateSpace = LinkedList();
StateSpace.addLast(InitState)
Run = 1;
while(Run)
%Visit->
Visit = StateSpace.removeFirst();
if rem(Steps, 50) == 0
disp(['-' num2str(Steps) '-'])
Visit
end
CheckSum = Visit == GoalState;
if(sum(sum(CheckSum)) == 4)
'Goal State Found ->'
Steps
Visit
Run = 0;
break;
end
TempQ = GenChildNodes(Visit, Passenger_boat, VectorSize);
for i=1:TempQ.size
Containers = TempQ.removeFirst();
if Containers(1, 3) > DepthLim
StateSpace.addLast(Containers);
else
StateSpace.addFirst(Containers);
end
end
Steps = Steps + 1;
end
function y = GenChildNodes(InState, boatLim, VectorSize)
y = LinkedList();
%보트 인원
for cnt=1:boatLim
%Missionary
for cntsub=1:cnt
Temp = InState;
MNumber = Temp(1, 1);
if MNumber >= cntsub
RightNum = Temp(1, 2);
RightNum = RightNum + cntsub;
Temp(1, 2) = RightNum;
Temp(1, 1) = VectorSize - RightNum;
CNumber = Temp(2, 1);
if CNumber >= cnt - cntsub
RightNum = Temp(2, 2);
RightNum = RightNum + (cnt - cntsub);
Temp(2, 2) = RightNum;
Temp(2, 1) = VectorSize - RightNum;
if feasibleSol(Temp)
Temp(:, 3) = Temp(:, 3) + 1;
y.addLast(Temp)
end
end
end
end
end
%Cannibal
Temp = InState;
Number = Temp(2, 1);
if Number >= cnt
RightNum = Temp(2, 2);
RightNum = RightNum + cnt;
Temp(2, 2) = RightNum;
Temp(2, 1) = VectorSize - RightNum;
if feasibleSol(Temp)
Temp(:, 3) = Temp(:, 3) + 1;
y.addLast(Temp)
end
end
end
function y = feasibleSol(ValidState)
%1행 - 선교사 2행 - 식인종
Missionary = ValidState(1, :);
Cannibal = ValidState(2, :);
CheckSum = Cannibal > Missionary;
if sum(CheckSum) == 0
y = true;
else
if Missionaray(CheckSum) == 0
y = true;
else
y = false;
end
end
end
