MATLAB 적대적 탐색을 이해하여 Tic-Tac-Toe를 구현해보자

1. Adversarial Search

1.1. Games

저희가 살면서 상대방에게 Adversarial,적대적인감정을 느낄 때가 언제 있을까요? 심지어 반복적으로 자주 있다면 계속 이기고 싶을겁니다. 피할 수 없다면요. 인류 기술의 발전은 아이러니하게도 전쟁이 큰 역할을 했다는 얘기 들어보신 적 있으신가요? 이제부터 얘기하는 게임은 전쟁도 게임이고 전쟁 속 전투들 또한 게임이라 합니다. 본문의 주제인 Adversarial Search는 주로 게임에 이용됩니다.

여기서 말하는 게임에는 어떤 요소를 가지고 있는 지 얘기해보겠습니다.

Multiagent environments
Initial states
Player
Action
Result
Terminal-test
Utility

1.1.1. States

State는 Feasible solution(가능해)의 집합입니다. 게임을 포함한 탐색에서 불가능한 상황을 제외한 전부라고 볼 수 있습니다. 예를 들어서 한 번에 5명까지 움직일 수 있는 배가 있다면, 랜덤으로 뽑은 0명에서 5명까지의 모든 상황을 정리해두면 이를 State space라고 합니다. 그리고 가능한 하나의 상황을 state라고 합니다. 그렇다면 6명으로 구성된 상황은 state space에 있을까요? Infeasible하기에 들어갈 수 없습니다.

1.1.2. Agent

Multiagent environments는 상호작용(Interaction)하는 둘 이상의 Agent가 있어야합니다. Agent는 Player이면서 게임에 임하는 사람이라고 할 수 있습니다. Agent(s)란 State - s에서 움직일 Agent에 대해서 정의를 얘기합니다.

1.1.3. Action

Action은 규칙이라 할 수 있습니다. 더 얘기하면 Action은 움직임을 표현한 집합입니다. 규칙과 움직임, 게임에서는 두 단어가 관련이 있습니다. 게임 속에서는 모든 Agents가 규칙에 의한 움직임만을 가집니다. 오목과 비유한다면 한 턴에 돌을 두, 세개 놓을 수 없으니 Action에는 한 개의 돌과 관련된 움직임이 들어가 있죠. 흰 돌을 두거나, 흑 돌을 두거나 입니다.

Action(s)란 State - s에서 움직임을 표현한 집합입니다.

1.1.4. Result

Result는 Action이후의 결과를 정의합니다. Action에 따라 유동적으로 변하므로 Transition model에 속합니다.

1.1.5. Terminal-test

종료 상태를 확인합니다.

1.1.6. Utility

점수에 해당합니다. 혹은 목표함수이며 이를 수치화된 형태로 얘기합니다.

1.2. Mini-max algorithm

1.2.1. Game tree

Adversarial Search를 얘기할 땐 Game을, Game 을 설명할 땐Game tree가 따라옵니다. 일반적인 tree라고 생각해도 됩니다. 크게 다르지 않습니다. 그러나 Level별로 자신, 상대방의 state를 번갈아서 표현합니다. 아래를 보시면 tic-tac-toe의 Game tree구조 일부입니다.

1.2.2. Mini-max function

Mini-max algorithm에서 사용되는 Optimal strategy는 아래의 수식에 의하여 행동이 결정됩니다. \(Minimax(s)=\begin{Bmatrix} utlity(s)\qquad if\ \ terminal-test(s)\\ max_a\ Minimax(result(s,a))\qquad if\ \ player(s) = max\\ min_a\ Minimax(result(s,a))\qquad if\ \ player(s) = min \end{Bmatrix}\) Min 노드에서는 Sibling node포함 min값을 선택합니다. Min노드의 level에는 상대방이 존재하고, Max노드에는 자신을 두며 Max값을 고릅니다.

말단 노드에서부터 위 계산식에 따라 점점 Root node를 향하며, 반복하여 올라가다보면 최적의 root node의 값이 결정됩니다.

이상함을 느끼신 분이 있나요?

1.2.3. Look-ahead

Tree는 기본적으로 Root node에서부터, Child node를 만들어가며 Optimal solution을 찾습니다. 그런데 Adversarial Search를 설명하며 Game tree의 구조는 말단에서 올라오는 Bottom-up의 형태를 띕니다. 그럼 구현하는 입장에서는 마음에 걸리는 게 있죠

어떻게? 얼마나? Game Tree의 Depth를 미리 알아야합니다. 수를 내다볼 때 Look-ahead라는 용어를 씁니다. 결국 모든 수를 다 보면 좋지만 매 턴마다 제한시간이 있는 경우 제한시간안에 응답을 보장못할 수 있습니다. 또한Look-ahead를 적게 설정해 첫 수부터 보지 못하면 전혀 쓸모없는 것일까요? 전혀 없을 수도 있지만, 있기는 합니다. 이러나 저러나 많은 수를 내다보는 게 좋긴 하다고 합니다.

Look-ahead는 많을 수록 좋습니다.

2. Implement

2.1. m,n,k-game

m,n,k-game은 mxn의 행렬에 k의 수를 맞추는 게임입니다. 예를 들어서 저희가 구현할 Tic-Tac-Toe는 3행, 3열에서 3개로 구성된 1줄을 맞추는 게임입니다. 그러니 3,3,3 game이라 할 수 있습니다.

2.2. Tic-Tac-Toe

두명이서 진행하는 게임이며 O와 X를 각 한명이 맡아 가로, 세로, 대각선 중 한 줄을 만드는 게임입니다. 그리고 선의 접점에 돌을 놓는 바둑이나 오목과는 다르게 면을 사용합니다. 그리고 아래처럼 비기는 상황도 나옵니다.

2.2. MATLAB code description

MATLAB 복사하기 쉽게된 전문은 제일 아래에 있습니다. 지금부터는 설명입니다.

참고로 여기엔 Mini-max algorithm이 적용되지 않았습니다. 왜냐하면 알고리즘이 적용안된 컴퓨터가 얼마나 수준낮은 패턴을 가지는 지 알려주기 위함이고 다음 포스터에는 게임트리 속 Mini-max algorithm이 적용된 컴퓨터와 게임합니다.

clc, clear
rng('shuffle',"simdTwister");

Row = 3;    % m
Column = 3; % n
Target = 3; % k
LookAhead = 10;
UsedSection = 'face';
State = zeros([Row Column]);

m, n, k-game대로 mxn의 사이즈와 k를 Target으로 정의합니다. 그리고 여기에선 사용하지는 않지만 LookAhead를 정의합니다. 이번에는 10 수(Game tree의 깊이) 앞을 보겠습니다. UsedSection은 오목이나 바둑처럼 선 위에 돌을 둘 것인지, 면에다가 돌을 둘 것인지 정의합니다. State는 돌을 둔 전체 상황(Result)이 들어갑니다.

%Visualization

%Field
figure
hold on
axis off
for m = 0:Column
    plot([m m],[0 Row], 'k','linewidth',2);
end
for n = 0:Column
    plot([0 Column], [n n], 'k','linewidth',2);
end

판을 그립니다.

% First turn
if rand > 0.5
    turn = 'me';
else
    turn = 'agent';
end

첫 판은 랜덤의 확률로 누가 먼저 할 지 결정합니다.

while true
    %Input
    if strcmp(turn, 'me')        
        inp = input('your position [Format = row, col] : ');
    else        
        inp(1) = randi(Row);
        inp(2) = randi(Column);
    end

같은 1행 1열은 [1 1]처럼 입력합니다. 컴퓨터 차례에는 랜덤으로 위치를 적용합니다.

if State(inp(1), inp(2)) == 0 && inp(1) <= Row && inp(2) <= Column
        if strcmp(turn, 'me')  
            Marker = 'x';
            myPoint = 1;
            turn = 'agent';
        else
            Marker = 'o';
            myPoint = 2;
            turn = 'me';   
        end
        State(inp(1), inp(2)) = myPoint;
    else
        'Invalid position!'
        continue;
    end

Feasible Check입니다. 비어있는 자리에, mxn사이즈 안에 있으면, 처리합니다.

[x, y] = Matrix2Coord(inp(1), inp(2), UsedSection, Row, Column);
    drawPos(x, y, Marker);

function [x, y] = Matrix2Coord(row, col, Used, m, n)
    Offset = 0;
    if strcmp(Used, 'face')
        Offset = 0.5;
    end
    x = (col - 1) + Offset;
    y = n - row + Offset;
end

행, 열로 입력받은 값을 그리기 위하여 x, y로 변환 합니다. TerminalTest를 통해서 끝낼지 말지 결정합니다.

T = TerminalTest(State, Target, myPoint, inp); 
    %Check Terminal-test
    if T == true
        break;
    end
    
    Checker = State == 0;
    if sum(Checker) == 0
        Disp('Draw Game');
        break;
    end
end
hold off

끝내는 단계입니다. State가 꽉 차면 Draw이고 TerminalTest가 끝내라면 끝냅니다.

function y = TerminalTest(A, Target, Val, Coord)
    y = false;
    checker = A(Coord(1), :) == Val;
    if sum(checker) == Target
        disp('made complete line in Column')
        y = true;
    end
    checker = A(:, Coord(2)) == Val;
    if sum(checker) == Target
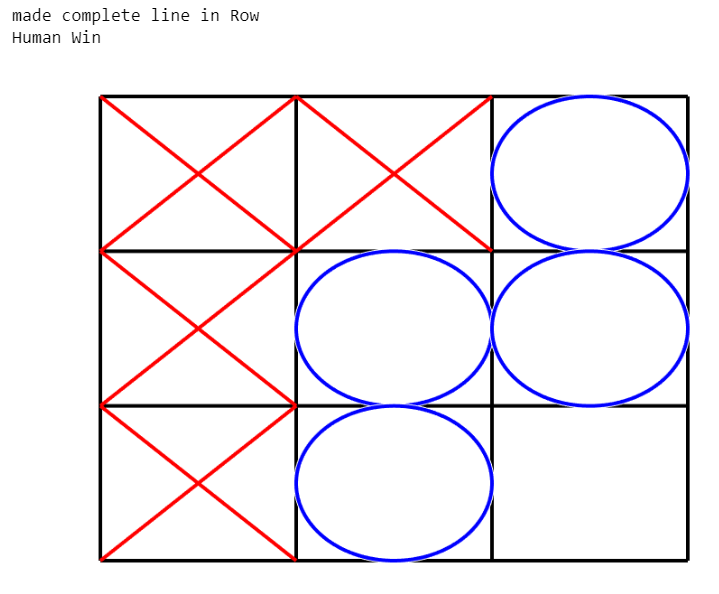
        disp('made complete line in Row')
        y = true;
    end
    checker = diag(A) == 1;
    if sum(checker) == Target
        disp('made complete line in Diagonal')
        y = true;
    end
    
    if y == true
        if Val == 1
            disp('Human Win')
        else
            disp('Computer Win')
        end
    end
end

조건문은 순서대로 1열이 완전히 만들어졌는지, 1행이 만들어졌는지, 대각선 1줄이 만들어졌는지 확인합니다. 만약 만들어졌다면 y=true를 만들어서 함수를 끝냅니다.

function rtnState = drawPos(x, y, Marker)
    if  strcmp(Marker, 'x') == true
        SymPos = [x-0.5 x+0.5;y-0.5 y+0.5; x-0.5  x+0.5;y+0.5 y-0.5];
        
        plot(SymPos(1,:), SymPos(2,:), 'r', 'linewidth',2);
        plot(SymPos(3,:), SymPos(4,:), 'r', 'linewidth',2);
        
    else
        viscircles([x, y],0.5,'Color','b');
    end
    
    rtnState = true;
end

x그릴지 o그릴지 보여줍니다.

2.3. MATLAB code 전문

clc, clear
rng('shuffle',"simdTwister");

Row = 3;    % m
Column = 3; % n
Target = 3; % k
LookAhead = 10;
UsedSection = 'face';
State = zeros([Row Column]);

%Field
figure
hold on
axis off
for m = 0:Column
    plot([m m],[0 Row], 'k','linewidth',2);
end
for n = 0:Column
    plot([0 Column], [n n], 'k','linewidth',2);
end


% First turn
if rand > 0.5
    turn = 'me';
else
    turn = 'agent';
end

while true
    
    %Input
    if strcmp(turn, 'me')        
        inp = input('your position [Format = row, col] : ');
    else        
        inp(1) = randi(Row);
        inp(2) = randi(Column);
    end
    
    if State(inp(1), inp(2)) == 0 && inp(1) <= Row && inp(2) <= Column
        if strcmp(turn, 'me')  
            Marker = 'x';
            myPoint = 1;
            turn = 'agent';
        else
            Marker = 'o';
            myPoint = 2;
            turn = 'me';   
        end
        State(inp(1), inp(2)) = myPoint;
    else
        'Invalid position!'
        continue;
    end
    [x, y] = Matrix2Coord(inp(1), inp(2), UsedSection, Row, Column);
    drawPos(x, y, Marker);
    T = TerminalTest(State, Target, myPoint, inp); 

    %Check Terminal-test
    if T == true
        break;
    end
    
    Checker = State == 0;
    if sum(Checker) == 0
        Disp('Draw Game');
        break;
    end
end
hold off

function rtnState = drawPos(x, y, Marker)
    if  strcmp(Marker, 'x') == true
        SymPos = [x-0.5 x+0.5;y-0.5 y+0.5; x-0.5  x+0.5;y+0.5 y-0.5];
        
        plot(SymPos(1,:), SymPos(2,:), 'r', 'linewidth',2);
        plot(SymPos(3,:), SymPos(4,:), 'r', 'linewidth',2);
        
    else
        viscircles([x, y],0.5,'Color','b');
    end
    
    rtnState = true;
end

function [x, y] = Matrix2Coord(row, col, Used, m, n)
    Offset = 0;
    if strcmp(Used, 'face')
        Offset = 0.5;
    end
    x = (col - 1) + Offset;
    y = n - row + Offset;
end

function y = TerminalTest(A, Target, Val, Coord)
    y = false;
    checker = A(Coord(1), :) == Val;
    if sum(checker) == Target
        disp('made complete line in Column')
        y = true;
    end
    checker = A(:, Coord(2)) == Val;
    if sum(checker) == Target
        disp('made complete line in Row')
        y = true;
    end
    checker = diag(A) == 1;
    if sum(checker) == Target
        disp('made complete line in Diagonal')
        y = true;
    end
    
    if y == true
        if Val == 1
            disp('Human Win')
        else
            disp('Computer Win')
        end
    end
end